本週(5/3)有來上課
此機構之曲桿長Rcm , 連桿Lcm,滑塊之偏置量為10cm等數據作分析。其中,R=10+(學號末二碼),L=R+5
計算曲桿和連桿的長度
學號b94611028
>> R=10+28
R =
38
>> L=R+5
L =
43
首先
利用講義的drawsldlinks來畫出靜態圖(設th1=0度,th2=60度)
第二桿為驅動桿
閉合型
>>drawsldlinks([10,R,L,10],0,60,1,0)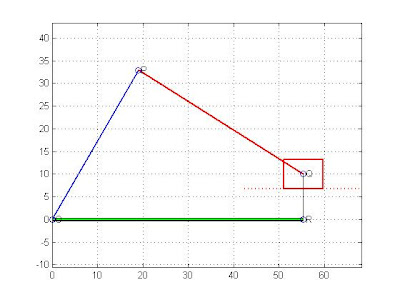
分支型
>>drawsldlinks([10,R,L,10],0,60,-1,0)
滑塊為驅動桿
閉合型
>>drawsldlinks([10,R,L,10],0,60,1,2)
分支型
>>drawsldlinks([10,R,L,10],0,60,-1,2)
以曲桿為驅動之連桿速度位置分析(閉合)
>>[val,form]=sldlink([10,R,L,10],0,60,10,0,1,0)
第一桿之軸向速度448.7 加速度1213.4
P點
位置 0.0190 + 0.0329i 速度380 (150度) 加速度3800 (120度).
Q點
位置 0.0554 + 0.0100i 速度448.7 (180度) 加速度1213.4(180度)
括號內為與水平之夾角
以滑塊為驅動之連桿速度位置分析(閉合)
>>[val,form]=sldlink([10,R,L,10],0,60,10,0,1,2)
求得
第一桿之軸向速度10 加速度0
P點
位置 -0.3150 + 0.2125i 速度29.8950 (55.9955度) 加速度0 (0度).
Q點
位置 0.1000 + 0.1000i 速度10 (76.3742度) 加速度31.8332 (0度)
括號內為與水平之夾角
接著我利用drawsldlimits來計算出機構運動之極限角
因為網路上的講義程式討論中並未提到r3≧r4≧0,且 r3+r4 ≧ r2情況
所以若直接用網路上程式計算本題極限角會出錯
因為程式將會直接執行下式
else
Qstart=0;Qstop=2*pi;
導致極限角圖出錯
更會連帶動畫圖執行不連續
故我修改了sld_angle_limits(r,theta1,linkdrive)
依照本題情況
在case 0(曲桿為驅動桿)中加入
elseif r3+r4>=r2 & r3>=r4 & r4>=0,
Qstart=-asin((r3-r4)/r2);
Qstop=pi+asin((r3-r4)/r2);
如此才能正確計算出極限角度
第二桿為驅動桿
閉合
>>drawsldlimits([10,R,L,10],0,1,0)
Qstart =
-60.2757
Qstop =
240.2757
分支
>> drawsldlimits([10,R,L,10],0,-1,0)
Qstart =
-60.2757
Qstop =
240.2757
滑塊為驅動桿
閉合
>>drawsldlimits([10,R,L,10],0,1,2)
Qstart =
-80.3803
Qstop =
80.3803
分支
>> drawsldlimits([10,R,L,10],0,-1,2)
Qstart =
-80.3803
Qstop =
80.3803
由上面四張圖可發現此狀況中分支型和閉合型其極限角之位置是相同的
接著試著以迴圈模式呼叫函數繪製每隔20度顯現的軌跡圖
分支
>> for th2=0:20:360;
drawsldlinks([10,R,L,10],0,th2,-1,0);
end;
閉合
>>for th2=0:20:360;
drawsldlinks([10,R,L,10],0,th2,1,0);
end
試驗的結果似乎只能適用在曲桿為驅動桿情況上
若以滑塊為驅動桿則並不能產生正確的軌跡,僅出現單一的位置圖(推測是程式輸入項和程式執行之變數不相符,故不能正確運作)
若使用網路講義之drawsldpaths
則不但2種情形之運動狀態皆可顯現,端點的運動軌跡也可以順利產生
第二桿為驅動桿
閉合
>>drawsldpaths(0,0,[10,R,L,10],0,10,0,1,100,0,0)
Qstart =
-60.2757
Qstop =
240.2757
分支
>>drawsldpaths(0,0,[10,R,L,10],0,10,0,-1,100,0,0)
Qstart =
-60.2757
Qstop =
240.2757
上兩圖更可直接看出分支和閉合的運動狀況
極限位置角相同,但是兩圖成對稱
滑塊為驅動桿
分支
>>drawsldpaths(0,0,[10,R,L,10],0,10,0,-1,100,2,0)
Qstart =
-80.3803
Qstop =
80.3803
閉合
>>drawsldpaths(0,0,[10,R,L,10],0,10,0,1,100,2,0)
Qstart =
-80.3803
Qstop =
80.3803
從上兩圖可以看到連桿的位置是由滑塊決定,當滑塊、曲桿、連桿為一條線時為其極限位置,此外分支與閉合兩種之運動主要在第三桿的位置,且明顯看出兩者綠色之軌跡並不相同
動態圖
使用網路講義之程式,因為以滑塊為驅動桿運動之程式不能執行
所以僅以曲桿為驅動桿製作動畫
閉合
>>move_sldpaths([10,R,L,10],0,0,3,0,10,0,1,0,4,100)
分支
>>move_sldpaths([10,R,L,10],0,0,3,0,10,0,-1,0,4,100)
接著設th1=10,以閉合型為例,觀察當r1與水平面傾斜,也就是若滑塊是在一個斜面上運動時的狀態
靜態圖(th2=60)
第二桿為驅動桿
>>drawsldlinks([10,R,L,10],10,60,1,0)
滑塊為驅動桿
>>drawsldlinks([10,R,L,10],10,60,1,2)
極限角
第二桿為驅動桿
>>drawsldlimits([10,R,L,10],10,1,0)
Qstart =
-50.2757
Qstop =
250.2757
滑塊為驅動桿
>>drawsldlimits([10,R,L,10],10,1,2)
Qstart =
-80.3803
Qstop =
80.3803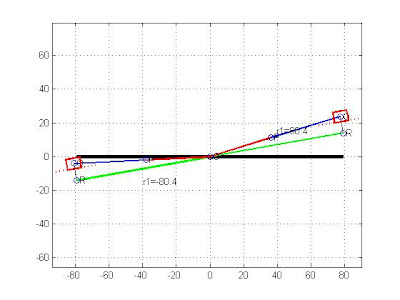
軌跡圖
第二桿為驅動桿
>>drawsldpaths(0,0,[10,R,L,10],10,10,0,1,100,0,0)
滑塊為驅動桿
>>drawsldpaths(0,0,[10,R,L,10],10,10,0,1,100,0,0)
動態圖
第二桿為驅動桿
>>move_sldpaths([10,R,L,10],0,0,3,10,10,0,1,0,4,100)
沒有留言:
張貼留言